Ciencia y tecnología

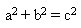
Una terna pitagórica son tres números enteros (1, 2, 3, 4, etc.) que cumplen el teorema de Pitágoras o dicho de otra manera que forman los lados de un triángulo rectángulo. Algebraicamente una terna pitagórica (a,b,c) son tres números enteros que cumplen el teorema de Pitágoras (ver imagen superior).

A a y b son los catetos y c la hipotenusa del triángulo rectángulo que forman.

La terna más conocida y más simple es (3, 4, 5) ya que 3*3 + 4*4 = 5*5. Hay otras ternas fáciles de obtener como (6, 8, 10) por la misma razón, 6*6 + 8*8 = 10*10.

Si (a,b,c) es una terna también lo será (d*a, d*b, d*c) donde d es cualquier número entero. En el ejemplo anterior d era igual a 2.

(3, 4, 5) es una terna en la que los dos catetos a y b son consecutivos, es decir b=a+1. Os propongo que obtengáis otra terna pitagórica con catetos consecutivos.

Pista: c = 29 (Solución en el primer comentario)

Copyleft: Miguel Angel Murillo Díaz.