FERMAT Y PITAGORAS

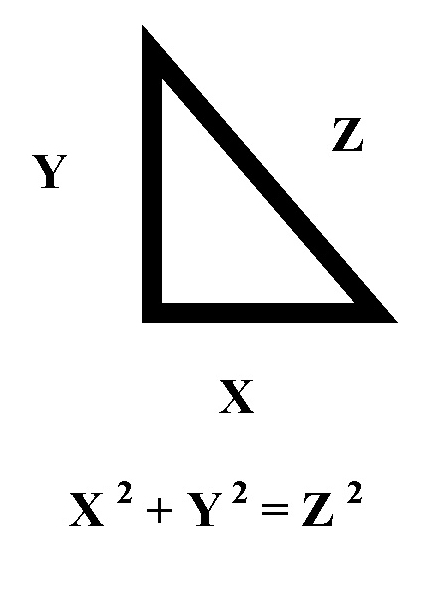
Si buscamos tres números naturales (0, 1, 2, 3, 4, 5, ...) que cumplan la condición de que la suma de los cuadrados de dos números es igual al cuadrado del otro número, no nos será difícil ya que estamos buscando x, y, z números naturales que verifican x^{2 +} y^{2 =} z². Por ejemplo los números 3, 4 y 5 verifican la igualdad y decimos que verifican el teorema de Pitágoras y también los números 6, 8 y 10 entre otros.

Pero ¿podemos encontrar tres números naturales x, y, z que verifiquen que x^{3 +} y^{3 =} z³?

¡¡ Encuentra la solución en el primer comentario de este artículo !!

Copyleft: Miguel Angel Murillo Díaz.

10 comentarios

[james - 02 de noviembre de 2012 - 00:14]

y cuales son los famosos numeros que resuelven el teorema??????

[rafael leal - 28 de mayo de 2010 - 09:23]

pues a mi me dio mucha curiosidad un capitulo de los simpsons (serie de fox)en el cual homero cae en la tercera dimension y aparece una formula demostrando que es posible cumplir la formula de pitagoras elevando al 12

[yop - 15 de diciembre de 2009 - 23:28]

n entendí nada de sus explicaciones, espero ke no sean profesores

[lilita - 06 de diciembre de 2009 - 16:28]

no entendi un choto

[pablocastillo - 14 de septiembre de 2006 - 02:44]

me interesa este tema

[RAUL SIERRA - 02 de septiembre de 2006 - 14:48]

UNA INTERPRETACION PITAGORICA DEL U.T.F. ARMONIZA AMBOS TEOREMAS.
EN www.raul-sierra.com.ve ESTA LA DEMOSTRACION MATEMATICA. TE AGRADEZCO TUS COMENTARIOS.
SALUDOS CORDIALES.

[Moises Galindo Herrera - 17 de agosto de 2006 - 20:40]

He trabajado varios meses tratandome de esplicar este teorema, exitosamente he descubierto que la afirmación de fermat es cierta, y los numeros que cumplien con cierta condición son numeros de grandes magnitudes, algun comentario, duda, o anecdota solo [e-mail]

[Moises Galindo Herrera - 17 de agosto de 2006 - 20:39]

He trabajado varios meses tratandome de esplicar este teorema, exitosamente he descubierto que la afirmación de fermat es cierta, y los numeros que cumplien con cierta condición son numeros de grandes magnitudes, algun comentario, duda, o anecdota solo escribanme...

[RAUL SIERRA - 14 de julio de 2006 - 23:55]

El Ultimo Teorema de Fermat es falso. En mi web lo explico en forma sencilla, con una prueba física, fórmulas e interpretación gráfica.

[Miguel Angel - 08 de marzo de 2006 - 00:32]

Solución:

Por mucho que busquemos, nunca encontraremos tres números que verifiquen x3 + y3 = z3. Pero tampoco los encontraremos para xn + yn = zn dónde n es mayor que 3.

Fermat fue una matemático francés del siglo XVII que escribió una nota en el margen de un libro diciendo que tenía la demostración de la imposibilidad de encontrar x, y, z pero que no tenía espacio suficiente para reproducirla.

La afirmación de Fermat dio lugar al llamado Teorema de Fermat e hizo que muchos matemáticos dedicasen parte de su vida a demostrar la imposibilidad de encontrar x, y, z que cumplan x3 + y3 = z3. Finalmente fue demostrada después de más de 300 años, por Andrew Wiles en 1995, utilizando herramientas matemáticas que ni siquiera Fermat conocía. ¿Realmente Fermat conocía la demostración? Nunca lo sabremos.