EL TRIANGULO DE PASCAL Y EL TRIANGULO DE SIERPINSKI
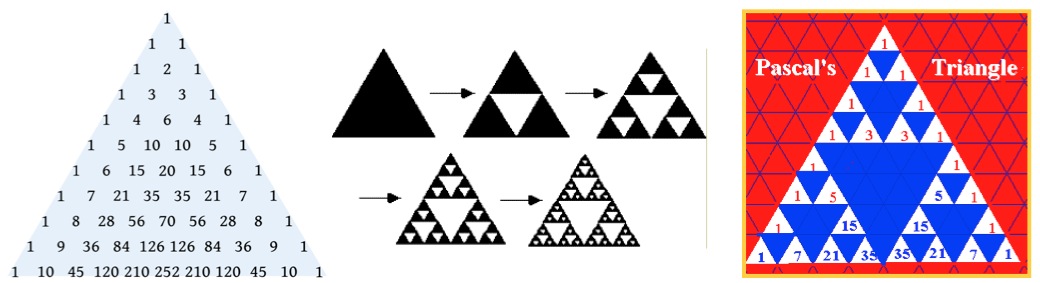
El triángulo de Pascal (matemático francés) es una construcción matemática muy simple pero con un sinfín de propiedades. En 1654, Blaise Pascal escribió un tratado sobre sus propiedades aritméticas. En la cúspide del triángulo si sitúa el número 1, en la fila inmediatamente inferior se colocan dos 1 a ambos lados. La siguiente fila tiene 1 en los extremos y los números interiores son la suma de los dos números inmediatamente superiores. Y así con todas las filas.
El triángulo de Sierpinski (matemático polaco) es un fractal que se construye a partir de un triángulo cualquiera. Si unimos los puntos medios de cada lado, tendremos al triángulo dividido en cuatro triángulos. Entonces eliminamos el triángulo central en color blanco. Este proceso lo repetimos con los otros tres triángulos de color negro. Y así de manera indefinida. El resultado es una figura con la cualidad de que una pequeña parte de ella es igual a la totalidad de la figura.
Pero, ¿qué relación tienen los dos triángulos, cuando uno de ellos se construye aritméticamente y el otro geométricamente? Si nos fijamos en el triángulo de Pascal y eliminamos los números pares el triángulo de Pascal cumple el mismo patrón que el triángulo de Sierpinski.
Es un descubrimiento que pone de manifiesto la conexión entre diferentes materias de las matemáticas donde la repetición de patrones y armonía son habituales.
Copyleft: Miguel Angel Murillo Díaz.


 Tres amigos visitan una feria de libros usados. Uno de ellos compra 9 libros y otro 6 libros, todos ellos de la misma colección, gastándose todo su dinero. El tercero no se compra ningún libro, pero al cabo de varios días se arrepiente y les propone repartir los libros entre los tres a partes iguales y a cambio les da 30 euros a sus amigos.
Tres amigos visitan una feria de libros usados. Uno de ellos compra 9 libros y otro 6 libros, todos ellos de la misma colección, gastándose todo su dinero. El tercero no se compra ningún libro, pero al cabo de varios días se arrepiente y les propone repartir los libros entre los tres a partes iguales y a cambio les da 30 euros a sus amigos.  Disponemos de un tablero de ajedrez al que le faltan las dos casillas blancas de las esquinas y de 31 fichas dobles donde cada una ocupa exactamente dos casillas del tablero.
Disponemos de un tablero de ajedrez al que le faltan las dos casillas blancas de las esquinas y de 31 fichas dobles donde cada una ocupa exactamente dos casillas del tablero.